Множества (set и frozenset) в Python

Множества – самая сложная для понимания структура данных, если у вас нет высшего математического образования. Освоить базовые операции со множествами – просто, но как только вы познакомитесь с математическими операциями, вас будет преследовать простой, но навязчивый вопрос: «А зачем это вообще нужно?». Ниже мы на этот вопрос постараемся ответить, пока будем рассказывать про все функции множеств.

Что такое «множество»?

Зачем множества нужны?

Базовые операции над множествами

Математические операции над множествами

Поиск подмножеств

Что нужно запомнить

Что такое «множество»?

В математике множество – это набор любых уникальных объектов. Множества в Python – это тип данных, который позволяет собирать математические множества. Свойства множеств в Python:

Хранят только уникальные объекты. Объекты во множествах не могут повторяться – если вы во множество {1, 2, 3, 4, 5} попытаетесь добавить «3», множество не изменится.
Изменяемы (set) или неизменяемы (frozenset). Set позволяет добавлять элементы и удалять их, frozenset – не позволяет. В остальном они аналогичны друг другу. Говоря о множествах ниже, мы будем подразумевать изменяемые множества (set) – если нужно будет что-то рассказать конкретно о frozenset, мы отдельно это подчеркнем.
Неупорядочены. Если вы последовательно добавляете во множество числа 1, 2, 3, 4 и 5 – Python не гарантирует, что при переборе множества через for вы получите эти числа именно в том порядке, в котором их добавили. Из этого правила есть исключение: если вы не изменяли множество, то результат перебора через последующий for будет таким же, как в предыдущем for; но писать код, опирающийся на это – крайне плохая практика, избегайте этого.
Могут хранить только неизменяемые данные. Если говорить более точно, то множества могут хранить только hashable-объекты, но это – практически то же самое, что и неизменяемые. Получается, что из базовых типов во множество можно поместить только числа (включая дробные), строки, кортежи и frozenset.

Последнее связано с тем, что в оперативной памяти множество превращается в хэш-число – уникальную последовательность данных. Преобразование множества в хэш имеет 2 важных последствия:

Множества занимают много места. Данные во множестве будут занимать примерно в 2-3 раза больше оперативной памяти, чем те же данные в списке.
Множества работают крайне быстро. Если нужно проверить принадлежность элемента множеству – set справится с этим в 100-1000 раз быстрее, чем список.

Зачем множества нужны?

Само по себе множество – это просто забавная структура данных со своими особенностями. Истинная мощь множеств раскрывается, когда нам нужно произвести какую-либо операцию над двумя множествами. Например: ваше приложение-маркетплейс собирает данные о предпочтениях пользователей для того, чтобы впоследствии решить, на какие товары выдавать скидки. Все данные обо всех пользователях хранятся в базе данных. Пришла пора эти данные проанализировать, и перед вами стоит задача: для каждого пользователя в базе нужно взять все категории, в которых пользователь делал покупки, и найти самую частую (популярную). Данные в базе хранятся не очень продуманно – номера категорий, которыми интересовался пользователь, записаны в string через запятую.

Кто и зачем придумал такую неудобную базу – другой вопрос, вам сейчас нужно решить практическую задачу на основе имеющихся инструментов. Распарсить строку конкретного пользователя – не проблема, но что дальше? Вы можете передавать результат парсинга в функцию, которая будет подсчитывать упоминания каждой категории и хранить счетчики в отдельном списке, но:

Код будет раздутым.
Подсчет займет 80 часов, потому что у вас – 100 000 000 записей.

Вот как эту задачу можно решить с помощью множеств – при условии, что «db_result» – это итератор, который последовательно подкидывает результат пользователя из базы данных:

result = set()
for item in db_result:
result |= set(item.split(‘,’))

И работать это будет в 100 раз быстрее – весь поиск займет около 50 минут, а не 80 часов.

Базовые операции над множествами

Создать

Если вам нужно создать пустое множество – используйте встроенную функцию языка set или frozenset:

test_set = set()
test_frozenset = frozenset()

«Знак» множества – фигурные скобки, как вы увидите в дальнейшем. Такой же знак – у словарей (у разработчиков закончились скобки для обозначения структур данных). Когда вы пользуетесь фигурными скобками для создания непустой структуры – у интерпретатора не возникает вопросов, потому что во множествах хранятся одиночные данные, а в словарях хранятся парные. А вот в случае с «{}» понять, какая именно структура данных здесь подразумевалась, не получается, поэтому разработчики решили, что «{}» – это словарь, а для множеств нужно использовать set().

Самый простой способ создать непустое множество – просто перечислить данные в скобках:

test_set = {1, 4, 2, 5, 3}

В большинстве случаев множество нужно создать на основе какой-то другой итерируемой структуры данных – в этом случае структуру данных нужно передать в функцию set() или frozenset(), и язык все сделает за вас:

Как и в случае с другими функциями, создающими структуры данных – если вы передадите в set() словарь, из него возьмутся только ключи. Чтобы передать во множество пары «ключ:значение» в кортежах, вам нужно использовать встроенный метод словарей .items():

Наконец, последний способ создания множеств – генераторы (set comprehension). Python позволяет описать содержимое множества через короткую запись for:

{действие for переменная in последовательность if условие}

Писать условие не обязательно. Например, мы хотим создать множество кубов для всех чисел от 1 до 100, если число делится на 3 без остатка:

Прочитать

Поскольку данные во множествах хранятся в произвольном порядке – мы не можем получить к ним доступ по индексу. Остается 2 инструмента: in и pop(). In работает как для set, так и для frozenset – он позволяет проверить наличие элемента во множестве, возвращает True или False:

pop() – это встроенный метод множества, который удаляет случайное значение и возвращает его. Этот метод может быть полезен, если мы, например, пишем рандомизатор для поиска победителя в конкурсе. Метод работает только с set(); прочитать конкретное значение можно единожды, потому что оно удаляется из множества:

Добавить

Если нам нужно добавить один элемент – пользуемся встроенным методом add(), если нужно добавить несколько элементов – пользуемся встроенным методом update(), которому передаем итерируемый объект:

С frozenset все это не работает. Еще один способ добавления элементов – через объединение множеств, но про это мы расскажем позже.

Удалить

Все методы этого подраздела работают только с set. Про метод pop() мы уже рассказывали выше – он удаляет случайное значение и возвращает его. Есть еще 3 метода для удаления данных из множества:

remove(). Удаляет элемент, если такого элемента во множестве нет – remove() генерирует исключение.
discard(). То же, что и remove(), но не генерирует исключение, если элемента не оказалось.
clear(). Удаляет вообще все значения из множества.

К слову, проверить наличие элементов во множестве можно либо через bool(), либо через len() – нужно передать множество этим функциям, bool() при пустом множестве вернет False, len() вернет 0.

Перебрать

Множество перебирается так же, как и другие итерируемые объекты – через for:

Как мы уже отмечали выше – множества не являются упорядоченными, поэтому не стоит писать алгоритмы, полагающиеся на последовательность добавленных элементов.

Сортировать

Если нужно отсортировать множество – пользуйтесь встроенной в язык функцией sorted:

Обратите внимание – результатом сортировки множества является список, что логично, поскольку ввиду неупорядоченности множество не может быть отсортированным по определению.

Математические операции над множествами

Что это?

Вам будет намного проще понимать математические операции над множествами, если сначала вы узнаете, зачем они нужны. Все математические операции над множествами сводятся к выявлению между ними отношений: какие элементы присутствуют в обоих множествах, какие есть только в одном, входят ли все элементы одного множества в другое (является ли одно множество подмножеством другого) и так далее. Все эти операции оказываются очень удобными, когда нам нужно выяснить отношения между двумя массивами данных – например, если мы ищем самую популярную категорию товаров как в примере выше.

Математические операции, которые можно совершать над множествами: объединение, пересечение, разность и симметрическая разность, результатом любой операции будет пустое или непустое множество. Кроме того, можно выяснить, является ли одно множество подмножеством другого – или же они абсолютно равны, то есть в обоих присутствуют одинаковые элементы. Все эти операции и отношения крайне удобно показывать на диаграммах Венна – диаграммах пересекающихся кругов, ниже мы будем использовать их для наглядной иллюстрации.

Объединение

Результатом объединения двух множеств является объединенное множество – в нем есть элементы и из первого, и из второго множеств:

Есть 2 формы записи для объединения:

set3 = set1.union(set2). Короткая запись: set3 = set1 | set Можно поменять set1 и set2 местами – суть не изменится.
update(set2). Короткая запись: set1 |= set2. Результат записывается в set1.

Для методов – в качестве аргумента можно передать любой iterable, аргументов может быть несколько. Для короткой записи – операндами должны быть конкретно множества.

Пересечение

Результатом пересечения двух множеств является множество, в котором есть элементы, которые встретились и в первом, и во втором множествах:

Есть 2 формы записи для объединения:

set3 = set1.intersection(set2). Короткая запись: set3 = set1 & set2. Можно поменять set1 и set2 местами – суть не изменится.
intersection_update(set2). Короткая запись: set1 &= set2. Результат записывается в set1.

Разность

Результатом разности множества А и множества Б являются те элементы, которые присутствуют в А, но не присутствуют в Б:

Есть 2 формы записи для разности:

set3 = setdifference(set2). Короткая запись: set3 = set1 - set2. Если поменять множества местами – результат изменится.
difference_update(set2). Короткая запись: set1 -= set2. Результат записывается в set1.

Симметрическая разность

Результатом симметрической разности двух множеств является множество, в котором есть элементы, которые встретились либо только в первом, либо только во втором множестве:

Есть 2 формы записи для объединения:

set3 = set1.symmetric_difference(set2). Короткая запись: set3 = set1 ^ set Можно поменять set1 и set2 местами – суть не изменится.
symmetric_difference_update(set2). Короткая запись: set1 ^= set2. Результат записывается в set1.

Поиск подмножеств

Если у нас есть множество A, то подмножество – это такое множество B, все элементы которого есть в A:

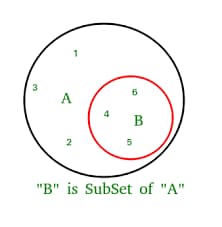
Если у нас есть множество А, то надмножество – это такое множество B, которое включает в себя все элементы, присутствующие в A:

Если два множества содержат одни и те же элементы – они равны между собой. Строгое подмножество (надмножество) – это когда одно из множеств точно больше другого; нестрогое подмножество (надмножество) – это когда множества могут быть равны.

Наконец, последнее из возможных отношений – два множества, которые вообще не совпадают по своим элементам, они называются непересекающимися.

Теперь покажем, как все эти отношения находятся методами и знаками сравнения:

Подмножество. Метод: set1.issubset(set2). Короткая запись: set1 < set2 (строгое подмножество); set1 <= set2 (нестрогое подмножество). Возвращает True, если set1 является подмножеством
Надмножество. Метод: set1.issuperset(set2). Короткая запись: set1 > set2 (строгое надмножество); set1 >= set2 (нестрогое надмножество). Возвращает True, если set1 является надмножеством set
Равенство. set1 == set Возвращает True, если множества равны.
Проверка непересекающихся множеств. setisdisjoint(set2). Вернет True, если множества не пересекаются.

Методы принимают любой iterable объект, короткая же запись требует, чтобы обоими операндами были множества.

Что нужно запомнить

По пунктам:

Множество – это неупорядоченная структура данных, все элементы которой уникальны.
Set – множество, которое можно изменять; frozenset – множество, которое нельзя изменять.
Создать пустое множество можно только через функцию – set() или frozenset().
Множество заключено в {фигурные скобки}.
Математические операции над множествами – объединение, пересечение, разность, симметрическая разность.
Отношения между множествами – подмножество, надмножество, равенство, отсутствие пересечения.
Множества едят много оперативной памяти, но крайне быстро работают – в сотни раз быстрее, чем списки.

Сравни.руОнлайн курсыПутеводительМножества (set и frozenset) в Python